基于强化学习的贪吃蛇游戏(一)——强化学习基础

最近在帮导师完成他教材的编纂，其中我的部分是使用强化学习来完成贪吃蛇游戏。在博客里记录下整个过程。

$$\log_{😄}😅=💧$$

强化学习基本概念

广泛的讲，强化学习是机器通过与环境交互来实现目标的一种计算方法。机器和环境的一轮交互是指，机器在环境的一个状态下做一个动作决策，把这个动作作用在环境当中，这个环境发生相应的改变并且将相应的奖励反馈和下一轮状态传回机器。这种交互式迭代进行的，机器的目标是最大化在多轮交互过程中获得的累计奖励的期望。强化学习用智能体这个概念来表示做决策的机器。相比于有监督学习中的“模型”，强化学习中的“智能体”强调机器不但可以感知周围的环境信息，还可以通过做决策来直接改变这个环境，而不只是给出一些预测信号。

在每一轮交互中，智能体感知到环境目前所处的状态，经过自身的计算给出本轮的动作，将其作用到环境中；环境得到智能体的动作后，产生相应的即时奖励信号并发生相应的状态转移。智能体则在下一轮交互中感知到新的环境状态，依次类推。

这里，智能体有3种关键要素，即感知、决策和奖励。

• 感知。智能体在某种程度上感知环境的状态，从而知道自己所处的现状。例如，下围棋的智能体感知当前的棋盘状况；无人车感知周围道路的车辆、行人和红绿灯等情况；机器狗通过摄像头感知面前的图像，通过脚底的力学传感器来感知地面的摩擦功率和倾斜度等情况。
• 决策。智能体根据当前的状态计算出达到目标需要采取的动作的过程叫做决策。例如，针对当前的棋盘决定下一颗落子的位置；针对当前的路况，无人车计算出方向盘的角度和刹车、油门的力度；针对当前收集到的视觉和力学信号，机器狗给出4条腿的齿轮的角速度。策略是智能体最终体现出的智能形式，是不同智能体之间的核心区别。
• 奖励。环境根据状态和智能体采取的动作，产生一个标量信号作为奖励反馈。这个标量信号衡量智能体这一轮动作的好坏。例如，围棋博弈是否胜利；无人车是否安全、平稳且快速的行驶；机器狗是否在前进而没有摔倒。最大化累计奖励期望是智能体提升策略的目标，也是衡量智能体策略好坏的关键指标。

从以上分析可以看出，面向决策任务的强化学习和面向预测任务的有监督学习在形式上是有不少区别的。首先，决策任务往往涉及多轮交互，即序贯决策；而预测任务总是单轮的独立任务。如果决策也是单轮的，那么它可以转化为“判别最优动作”的预测任务。其次，因为决策任务是多轮的，智能体就需要在每轮做决策时考虑未来环境相应的改变，所以当前轮带来最大奖励反馈的动作，在长期来看并不一定是最优的。

马尔可夫决策过程

强化学习中的核心理论框架之一是马尔可夫决策过程（Markov Decision Process, MDP），它为智能体在交互式环境中建模提供了数学基础。一个MDP可以用一个五元组$\left \langle \mathcal{S},\mathcal{A},\mathcal{P},r,\gamma \right \rangle$来描述，其中每个部分定义了强化学习问题中的关键组成要素：

• $\mathcal{S}$（状态空间）：表示环境中所有可能的状态集合，智能体通过感知环境可以确定当前的状态。
• $\mathcal{A}$（动作空间）：表示智能体在每个状态下可以选择的所有可能动作。
• $\mathcal{P}$（状态转移函数）：描述在当前状态$s \in \mathcal{S}$下执行动作$a\in \mathcal{A}$，环境转移到下一状态$s^\prime \in \mathcal{S}$的概率，记作$P(s^\prime|s,a)$。马尔可夫性质规定，状态的转移仅依赖于当前状态和动作，与之前的历史状态无关，即“无记忆性”。
• $r$（奖励函数）：定义智能体在状态$s$下执行动作$a$后，环境反馈的奖励值，记作$r(s,a)$。奖励是一个标量信号，用于衡量当前动作的优劣。智能体的目标是通过优化策略使累计奖励的期望最大化。
• $\gamma$（折扣因子）：介于0和1之间的一个因子，用于权衡即时奖励和长期奖励的重要性。当$\gamma$趋近于0时，智能体更关注当前的即时奖励；当$\gamma$趋近于1时，智能体更关注未来的长期奖励。

在马尔可夫决策过程中，通常存在一个智能体来执行动作，从而主动决策以获得更大的奖励。马尔可夫决策过程是一个与时间相关的不断进行的过程，在智能体和环境MDP之间存在一个不断交互的过程。一般而言，它们之间的交互是如图1的循环过程：智能体根据当前状态$S_t$选择动作$A_t$；对于状态$S_t$和动作$A_t$，MDP根据奖励函数和状态转移函数得到$S_{t+1}$和$R_t$并反馈给智能体。智能体的目标是最大化得到的累计奖励。智能体根据当前状态从动作的集合$\mathcal{A}$中选择一个动作的函数，被称为策略。随着上述交互过程持续进行，最终智能体通过试错学习找到一个最优策略，使得在任意状态下所采取的动作能够最大化累计奖励的期望值。

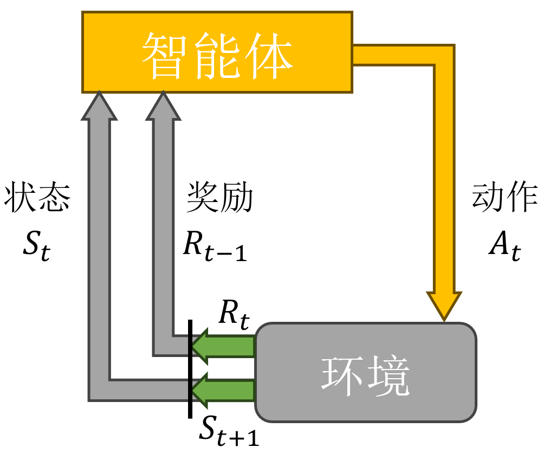
图1: 马尔可夫决策过程示意图

策略

智能体的策略通常用字母$\pi$表示。策略$\pi(a|s)=P(A_t=a|S_t=s)$是一个函数，表示在输入状态$s$情况下采取动作$a$的概率。当一个策略是确定性策略时，它在每个状态时只输出一个确定性的动作，即只有该动作的概率为 1，其他动作的概率为 0；当一个策略是随机性策略时，它在每个状态时输出的是关于动作的概率分布，然后根据该分布进行采样就可以得到一个动作。在 MDP 中，由于马尔可夫性质的存在，策略只需要和当前状态有关，不需要考虑历史状态。

状态价值函数

在一个马尔可夫决策过程中，从第$t$时刻状态$S_t$开始，直到终止状态时，所有奖励的衰减之和称为回报$G_t$，公式如下：

$$G_t = R_{t} + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots = \sum_{k=0}^{\infty} \gamma^{k} R_{t+k}$$

在马尔可夫决策过程中，一个状态的期望回报（即从这个状态出发的未来累积奖励的期望）被称为这个状态的价值。所有状态的价值就组成了价值函数，价值函数的输入为某个状态，输出为这个状态的价值。我们将价值函数写成$V^\pi(s)=\mathbb{E}[G_t|S_t=s]$，展开为：

$$\begin{aligned} V^\pi(s) &= \mathbb{E}[G_t|S_t=s] \\ &= \mathbb{E}[R_{t} + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots | S_t=s] \\ &= \mathbb{E}[R_{t} + \gamma (R_{t+1} + \gamma R_{t+2} + \cdots) | S_t=s] \\ &= \mathbb{E}[R_{t} + \gamma G_{t+1} | S_t=s] \\ &= \mathbb{E}[R_{t} + \gamma V^\pi(S_{t+1}) | S_t=s] \\ \end{aligned}$$

动作价值函数

在MDP中，由于动作的存在，我们额外定义一个动作价值函数。我们用$Q^\pi(s,a)$表示在 MDP 遵循策略$\pi$时，对当前状态$s$执行动作$a$得到的期望回报：

$$Q^\pi(s,a) = \mathbb{E}_{\pi}[G_t|S_t=s,A_t=a]$$

状态价值函数与动作价值函数之间的关系：在使用策略$\pi$ 时，状态$s$的价值等于在该状态下基于策略$\pi$采取所有动作的概率与相应的价值相乘再求和的结果：

$$V^\pi(s) = \sum_{a \in \mathcal{A}} \pi(a|s)Q^\pi(s,a)$$

使用策略$\pi$时，状态$s$下采取动作$a$ 的价值等于即时奖励加上经过衰减后的所有可能的下一个状态的状态转移概率与相应的价值的乘积：

$$Q^\pi(s,a) = r(s,a) + \gamma \sum_{s^\prime \in \mathcal{S}} P(s^\prime|s,a)V^\pi(s^\prime)$$

最优策略

强化学习的目标通常是找到一个策略，使得智能体从初始状态出发能获得最多的期望回报。我们首先定义策略之间的偏序关系：当且仅当对于任意的状态$s$都有$V^\pi(s) \ge V^{\pi^\prime}(s)$，记$\pi > \pi^\prime$。于是在有限状态和动作集合的MDP中，至少存在一个策略比其他所有策略都好或者至少存在一个策略不差于其他所有策略，这个策略就是最优策略。最优策略可能有很多个，我们都将其表示为$\pi^*(s)$。
最优策略都有相同的状态价值函数，我们称之为最优状态价值函数，表示为：

$$V^*(s) = \max_{\pi} V^\pi(s), \quad \forall s \in \mathcal{S}$$

同理，我们定义最优动作价值函数：

$$Q^*(s,a) = \max_{\pi} Q^\pi(s,a), \quad \forall s \in \mathcal{S}, a \in \mathcal{A}$$

为了使$Q^\pi(s,a)$最大，我们需要在当前的状态动作对$(s,a)$之后都执行最优策略。于是我们得到了最优状态价值函数和最优动作价值函数之间的关系：

$$Q^*(s,a) = r(s,a) + \gamma \sum_{s^\prime \in \mathcal{S}} P(s^\prime|s,a)V^*(s^\prime)$$

这与在普通策略下的状态价值函数和动作价值函数之间的关系是一样的。另一方面，最优状态价值是选择此时使最优动作价值最大的那一个动作时的状态价值：

$$V^*(s) = \max_{a \in \mathcal{A}} Q^*(s,a)$$

贝尔曼最优方程

根据$V^*(s)$和$Q^*(s,a)$的关系，我们可以得到贝尔曼最优方程：

$$V^*(s) = \max_{a \in \mathcal{A}} \left \{ r(s,a) + \gamma \sum_{s^\prime \in \mathcal{S}} P(s^\prime|s,a)V^*(s^\prime) \right \}$$

$$Q^*(s,a) = r(s,a) + \gamma \sum_{s^\prime \in \mathcal{S}} P(s^\prime|s,a) \max_{a^\prime \in \mathcal{A}} Q^*(s^\prime,a^\prime)$$

价值函数和贝尔曼方程是强化学习非常重要的组成部分，之后的一些强化学习算法都是据此推导出来的。

Q-learning算法

Q-learning 是一种基于值函数的无模型强化学习算法，通过直接学习最优动作价值函数（$Q$值）来实现最优策略的学习。它利用贝尔曼最优方程的递归特性，在智能体与环境交互的过程中不断更新$Q$值，最终逼近最优动作价值函数$Q^*(s,a)$，从而找到最优策略$\pi^*$。$Q$值的更新基于以下公式：

$$Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha \left [ r_t + \gamma \max_{a} Q(s_{t+1},a) - Q(s_t,a_t) \right ]$$

其中$\alpha$ 是学习率，控制$Q$值更新的步长。
Q-learning 算法的具体流程如下：

---

• 初始化$Q(s,a)$
• for 序列e=$1\to E$
  • 得到初始状态$s$
  • for 时间步$t=1\to T$ do
    • 用$\epsilon$-贪婪策略根据$Q$选择当前状态$s$下的动作$a$
    • 得到环境反馈的$r,s^\prime$
    • $Q(s,a) \leftarrow Q(s,a) + \alpha \left [ r + \gamma \max_{a^\prime} Q(s^\prime,a^\prime) - Q(s,a) \right ]$
    • $s \leftarrow s^\prime$
  • end for
• end for

---

我们可以用价值迭代的思想来理解 Q-learning，即 Q-learning 是直接在估计$Q^*$，因为动作价值函数的贝尔曼最优方程为

$$Q^*(s,a) = r(s,a) + \gamma \sum_{s^\prime \in \mathcal{S}} P(s^\prime|s,a) \max_{a^\prime \in \mathcal{A}} Q^*(s^\prime,a^\prime)$$

Q-learning 的更新并非必须使用当前贪心策略$\arg \max_a Q(s,a)$采样得到的数据，因为给定任意$(s,a,r,s^\prime)$都可以直接根据更新公式来更新$Q$，为了探索，我们通常使用一个$\epsilon$-贪婪策略来与环境交互。

ε-贪婪算法

在使用强化学习方法解决问题的实践中，我们往往需要考虑探索和利用的平衡问题。探索是指脱离当前策略去尝试新的动作，这次动作不一定会获得最大的奖励，但这种方案能够摸清其他动作带来的收益情况。在设计策略时，我们往往需要平衡探索和利用的次数，使得累计奖励最大化。一个比较常用的思路是在开始时做比较多的探索，在对整体情况都有比较准确的估计后，再进行利用。
完全贪婪算法即在每一时刻采取期望奖励估值最大的动作，这就是纯粹的利用，而没有探索，所以我们需要对完全贪婪算法进行一些修改，其中比较经典的一种方法为$\epsilon$-贪婪算法。$\epsilon$-贪婪算法在完全贪婪算法的基础上添加了噪声，每次以概率$1-\epsilon$选择以往经验中期望奖励估值最大的动作，以概率$\epsilon$随机选择一个动作，公式如下：

$$a_t = \begin{cases} \arg \max_{a \in \mathcal{A}} \hat{Q}(a) & \text{采样概率：} 1-\epsilon \\ \text{从} \mathcal{A} \text{中随机选择} & \text{采样概率：} \epsilon \end{cases}$$

随着探索次数的不断增加，我们对各个动作的奖励估计得越来越准，此时我们就没必要继续花大力气进行探索。所以在$\epsilon$-贪婪算法的具体实现中，我们可以令$\epsilon$随时间衰减，即探索的概率将会不断降低。但是请注意，$\epsilon$不会在有限的步数内衰减至 0，因为基于有限步数观测的完全贪婪算法仍然是一个局部信息的贪婪算法，永远距离最优解有一个固定的差距。

DQN算法

在 Q-learning 算法中，往往需要通过表格的方式维护每一个状态动作对$(s,a)$的$Q$值，表格中每一个动作价值$Q(s,a)$表示在状态$s$下选择动作$a$然后遵循某一策略预期能够得到的期望回报。然而，这种用表格存储动作价值的做法只在环境的状态和动作都是离散的，并且空间都比较小的情况下适用。当状态或者动作数量非常大的时候，这种做法就不适用了。例如本章所介绍的贪吃蛇游戏，存在非常多种状态，在计算机中存储这个数量级的$Q$值表格是不现实的。更甚者，当状态或者动作连续的时候，就有无限个状态动作对，我们更加无法使用这种表格形式来记录各个状态动作对的$Q$值。
对于这种情况，我们需要用函数拟合的方法来估计$Q$值，即将这个复杂的$Q$值表格视作数据，使用一个参数化的函数$Q_\theta$来拟合这些数据。很显然，这种函数拟合的方法存在一定的精度损失，因此被称为近似方法。本节介绍的 DQN（Deep Q-Network）算法便可以用来解决连续状态下离散动作的问题。
由于神经网络具有强大的表达能力，因此我们可以用一个神经网络来表示函数$Q$。若动作是离散的，我们可以将状态$s$输入到神经网络中，使其同时输出每一个动作的$Q$值。通常 DQN（以及 Q-learning）只能处理动作离散的情况，因为
在函数$Q$的更新过程中有$\max_a$这一操作。假设神经网络用来拟合函数$Q$的参数是$\omega$，即每一个状态$s$下所有可能动作$a$的$Q$值都能被表示为$Q_\omega(s,a)$。我们将用于拟合函数$Q$的神经网络称为 Q 网络，如图 2 所示。

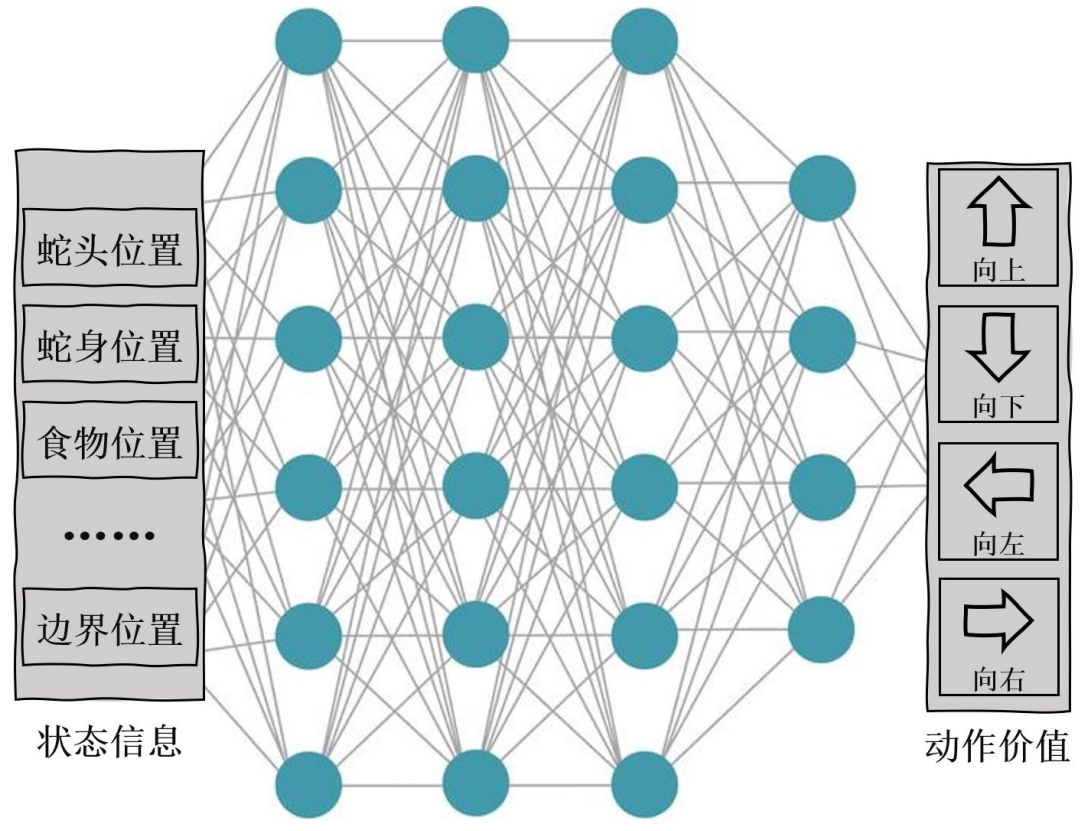
图2: DQN 网络示意图

那么 Q 网络的损失函数是什么呢？我们先来回顾一下 Q-learning 的更新规则：

$$Q(s,a) \leftarrow Q(s,a) + \alpha \left [ r + \gamma \max_{a^\prime} Q(s^\prime,a^\prime) - Q(s,a) \right ]$$

上述公式利用时序差分（temporal difference, TD）学习目标$r+\gamma \max_{a^\prime\in \mathcal{A}} Q(s^\prime,a^\prime)$来增量式更新$Q(s,a)$，也就是说要使$Q(s,a)$向TD误差目标$r+\gamma \max_{a^\prime\in \mathcal{A}} Q(s^\prime,a^\prime)$靠近。于是，对于一组数据$\left \{ (s_i,a_i,r_i,s_i^\prime) \right \}$，我们可以很自然的将 Q 网络的损失函数构造为均方误差的形式：

$$\omega^* = \arg \min_{\omega} \frac{1}{2N} \sum_{i=1}^N \left [ Q_\omega(s_i,a_i) - \left ( r_i + \gamma \max_{a^\prime \in \mathcal{A}} Q_\omega(s^\prime,a^\prime) \right ) \right ]^2$$

至此，我们就可以将 Q-learning 扩展到神经网络形式——深度 Q 网络算法。由于 DQN 是离线策略算法，因此我们可以在收集数据的时候使用一个$\epsilon$-贪婪策略来平衡探索和利用，将收集到的数据存储起来，在后续的训练中使用。DQN 中还有两个非常重要的模块——经验回放和目标网络，它们能够帮助 DQN 取得稳定、出色的性能。

经验回放

在一般的有监督学习中，假设训练数据是独立同分布的，我们每次训练神经网络的时候从训练数据中随机采样一个或若干个数据来进行梯度下降。随着学习的不断进行，每一个训练数据会被使用多次。在原来的 Q-learning 算法中，每一个数据只会用来更新一次$Q$值。为了更好地将 Q-learning 和深度神经网络结合，DQN 算法采用了经验回放方法。具体做法为维护一个回放缓冲区，将每次从环境中采样得到的四元组数据（状态、动作、奖励、下一状态）存储到回放缓冲区中，训练 Q 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。这么做可以起到以下两个作用：

1. 使样本满足独立假设。在 MDP 中交互采样得到的数据本身不满足独立假设，因为这一时刻的状态和上一时刻的状态有关。非独立同分布的数据对训练神经网络有很大的影响，会使神经网络拟合到最近训练的数据上。采用经验回放可以打破样本之间的相关性，让其满足独立假设。
2. 提高样本效率。每一个样本可以被使用多次，十分适合深度神经网络的梯度学习。

目标网络

DQN 算法最终更新的目标是让$Q_\omega(s,a)$逼近$r+\gamma \max_{a^\prime} Q_\omega(s^\prime,a^\prime)$，由于 TD 误差目标本身就包含神经网络的输出，因此在更新网络参数的同时目标也在不断地改变，这非常容易造成神经网络训练的不稳定性。为了解决这一问题，DQN 使用了目标网络的思想：既然在训练过程中 Q 网络的不断更新会导致目标不断发生改变，不如暂时先将 TD 误差目标中的 Q 网络固定住。为了实现这一思想，我们需要利用两套 Q 网络。

1. 原来的训练网络$Q_\omega(s,a)$，用于计算原来的损失函数$\frac{1}{2} \left [ Q_\omega(s,a) - \left ( r + \gamma \max_{a^\prime} Q_{\omega^-}(s^\prime,a^\prime) \right ) \right ]^2$中的$Q_\omega(s,a)$项，并且使用正常梯度下降方法来进行更新。
2. 目标网络$Q_{\omega^-}(s,a)$，用于计算原来的损失函数$\frac{1}{2} \left [ Q_\omega(s,a) - \left ( r + \gamma \max_{a^\prime} Q_{\omega^-}(s^\prime,a^\prime) \right ) \right ]^2$中的$r+\gamma \max_{a^\prime} Q_{\omega^-}(s^\prime,a^\prime)$项，其中$\omega^-$表示目标网络中的参数。如果两套网络的参数随时保持一致，则仍为原来不够稳定的算法。为了让更新目标更稳定，目标网络并不会每一步都更新。具体而言，目标网络使用训练网络的一套比较旧的参数，训练网络$Q_\omega(s,a)$在训练中的每一步都会更新，而目标网络的参数每隔$C$步才会与训练网络同步一次，即$\omega \leftarrow \omega^-$。这样做使得目标网络相对于训练网络更加稳定。
   综上所述，DQN 算法的具体流程如下：

---

• 用随机的网络参数$\omega$初始化$Q_\omega(s,a)$
• 复制相同的参数$\omega^- \leftarrow \omega$来初始化目标网络$Q_{\omega^-}(s,a)$
• 初始化经验回放池 $R$
• for 序列$e=1 \to E$ do：
  • 获取环境初始状态 1s
  • for 时间步$t=1 \to T$ do:
    • 根据当前网络$Q_\omega(s,a)$，以$\epsilon$-贪婪策略选择动作$a_t$
    • 执行动作$a_t$，获得回报$r_t$，环境状态变为$s_{t+1}$
    • 将$(s_t,a_t,r_t,s_{t+1})$存储在回放池$R$中
    • 若$R$中数据足够，从$R$中采样$N$个数据$\left \{ (s_i,a_i,r_i,s_{i+1}) \right \}_{i=1,\cdots,N}$
    • 对每个数据，用目标网络计算$y_i = r_i + \gamma \max_{a^\prime} Q_{\omega^-}(s_{i+1},a^\prime)$
    • 最小化目标损失$\frac{1}{N} \sum_{i} \left ( y_i - Q_\omega(s_i,a_i) \right )^2$，以此更新当前网络$Q_\omega$
    • 每$C$个时间步更新一次目标网络
  • end for
• end for

---

参考文献

张伟楠, 沈键, 俞勇. 动手学强化学习[M]. 北京：人民邮电出版社, 2022.