基于强化学习的贪吃蛇游戏(四)——基于DQN算法的智能体

在上一节中，我们通过Q-learning算法实现了一个能够自主学习玩贪吃蛇的强化学习智能体。虽然Q-learning算法在小规模的状态空间中表现良好，但它的局限性也非常明显。由于Q-table的大小随状态空间的增长呈指数级扩展，在面对更复杂或连续的环境时，Q-learning会因存储和计算的限制而难以适用。而贪吃蛇游戏的状态空间虽然经过简化，但仍然存在较大的扩展潜力。

在本章中，我们将基于前文提到的DQN算法设计一个智能体，并将其嵌入到贪吃蛇游戏中。我们会详细讲解DQN的实现步骤以及如何利用深度神经网络对贪吃蛇游戏进行训练。通过DQN，智能体将能够在更复杂的状态空间中学习到合适的策略。

$$\log_{😄}😅=💧$$

状态建模

不同于Q-learning直接将状态映射到Q-table的索引，DQN需要将游戏状态表示为一个张量，作为神经网络的输入。通过这种方式，DQN能够处理更复杂的状态空间，并通过深度神经网络学习状态与动作之间的映射。
在本项目中，我们将贪吃蛇游戏的状态建模为一个$3 \times 12 \times 12$的输入张量，如图1所示：

• 通道1：蛇头位置。使用一个$12 \times 12$的矩阵表示蛇头的位置，矩阵中蛇头所在的格子值为1，其余格子值为0。
• 通道2：蛇身位置。使用一个$12 \times 12$的矩阵表示蛇身的位置（不包括蛇头），矩阵中蛇身所在的格子值为1，其余格子值为0。
• 通道3：食物位置。使用一个$12 \times 12$的矩阵表示食物的位置，矩阵中食物所在的格子值为1，其余格子值为0。
  通过将这些信息合并到一个$3 \times 12 \times 12$的张量中，我们可以完整地表示游戏当前的状态。这样，神经网络可以通过卷积层捕捉空间信息，并对状态进行处理。

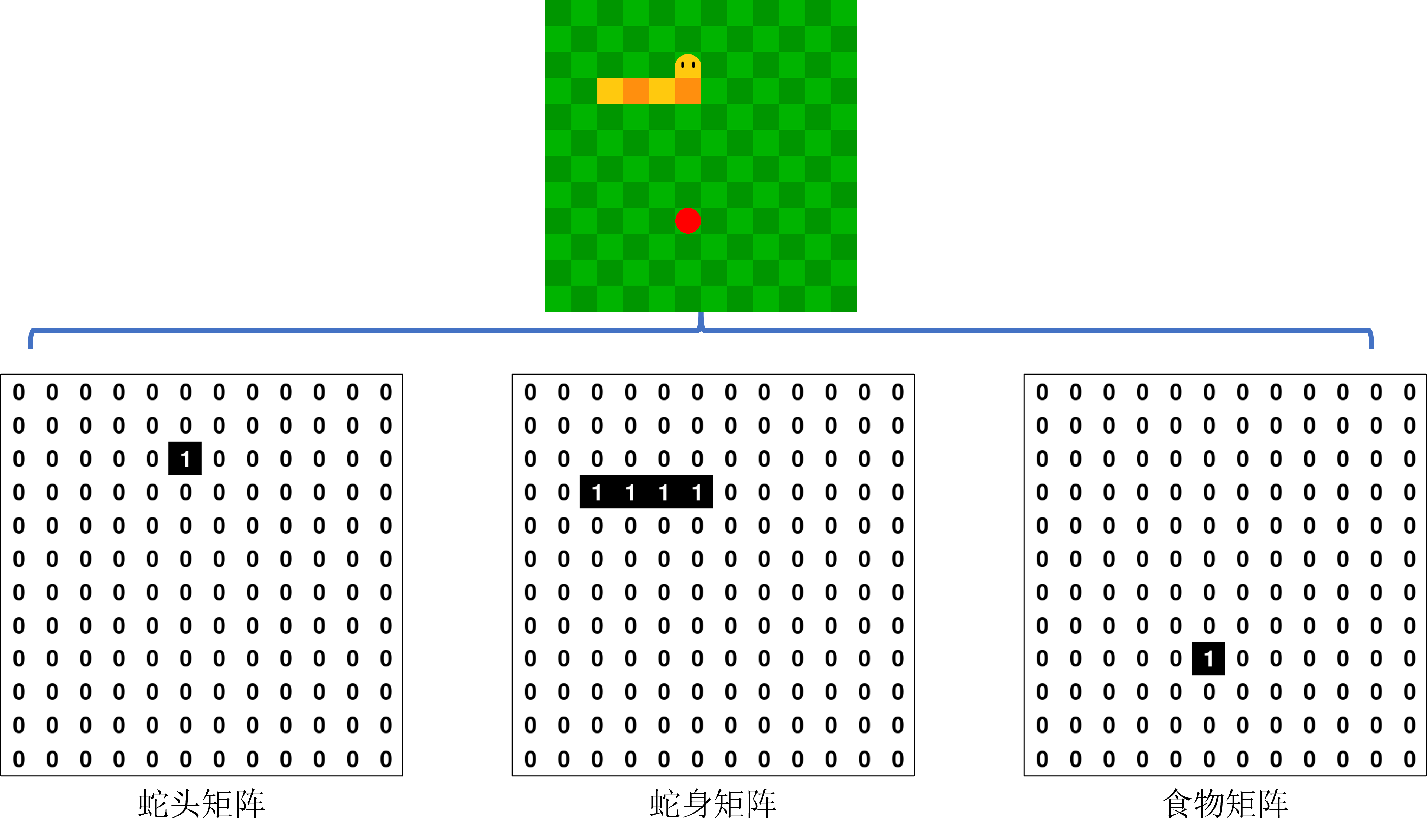
图1 将游戏信息建模为三个矩阵

网络设计

在DQN智能体中，神经网络的设计至关重要，它直接决定了智能体的学习能力和效率。我们采用了一个卷积神经网络作为$Q$值的近似函数，专门处理输入状态张量，提取空间特征，并最终输出动作的$Q$值。网络结构主要包括卷积层和全连接层两部分，整体结构如图2所示。

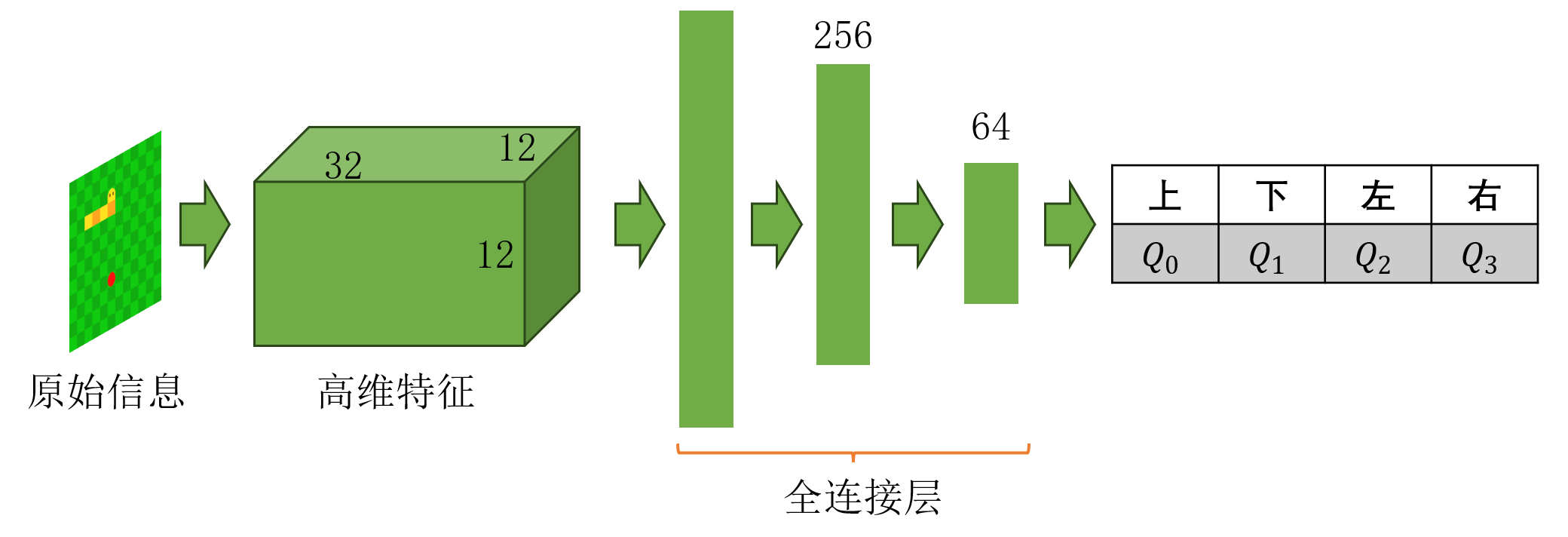
图2 神经网络结构设计

状态特征首先进入卷积层部分。输入的状态张量具有3个通道，分别表示蛇头、蛇身和食物的位置。为了提取这一输入中的局部空间特征，我们设计了一个卷积核大小为3的卷积层，将输入3个通道映射为32个特征通道。卷积层的输出尺寸保持为$12 \times 12$。在这里，考虑到蛇头对位置十分敏感，我们采用-1作为边界填充的值，以增强智能体对边界的感知。在卷积操作后，我们使用线性整流（ReLU）激活函数，为网络引入非线性表达能力，从而帮助模型更好地拟合复杂的状态与动作价值之间的关系。
卷积层的输出被展平为一维向量后，进入全连接层部分。通过一系列全连接层进一步压缩特征维度。第一层全连接层将卷积特征映射到256个隐藏单元，第二层将256映射到64，最后一层输出4个值，分别对应智能体在当前状态下每个动作（上、下、左、右）的$Q$值。这种逐步压缩的结构能够有效提取卷积特征中的重要信息，并将其转化为动作的价值预测。
我们通过创建Net类实现网络的定义，它继承自torch.nn.Module从而实现网络的前向传播与反向传播。

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv = nn.Sequential(
            nn.ConstantPad2d(1, -1),
            nn.Conv2d(3, 32, kernel_size=3), # 32x12x12
            nn.ReLU(),
        )
        self.fc = nn.Sequential(
            nn.Flatten(),
            nn.Linear(32 * 12 * 12, 256),
            nn.ReLU(),
            nn.Linear(256, 64),
            nn.ReLU(),
            nn.Linear(64, 4),
        )
    
    def forward(self, x):
        feat = self.conv(x)
        return self.fc(feat)

智能体初始化

在基于DQN的智能体中，除去在5.4节中提及的超参数，我们需要额外增加了一个容量为50000的经验回放池，用于存储智能体的经验（包括状态、动作、奖励和下一状态）。这一机制允许智能体从过去的经验中学习，通过小批量采样实现数据的重复利用，减少样本间的相关性，提升学习的稳定性。
DQN智能体在初始化过程中，需要创建评估网络和目标网络。评估网络用于估计当前状态下的$Q$值，并直接参与训练；目标网络则用于生成目标$Q$值，其参数每隔一定的时间步从评估网络同步一次。正如前文所提到的，目标网络的设计能够有效缓解训练中的不稳定性，避免目标值直接依赖自身估计而导致的发散问题。除此之外，智能体的训练使用Adam优化器更新评估网络的参数；损失函数采用均方误差，用来最小化评估网络的$Q$值与目标$Q$值之间的误差。

class DQN(nn.Module):
    MEMORY_SIZE = 50000
    def __init__(self):
        super(DQN, self).__init__()
        self.learning_rate = 1e-3
        self.gamma = 0.95
        self.epsilon = 0.1
        self.epsilon_decay = 0.999
        self.replay_memory = []
        self.batch_size = 64
        self.time_step = 0
        self.eval_net = Net()
        self.target_net = Net()
        self.init_parameters()
        self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=self.learning_rate)
        self.loss_func = nn.MSELoss()
  
    def init_parameters(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
            elif isinstance(m, nn.BatchNorm2d):
                nn.init.constant_(m.weight, 1)
                nn.init.constant_(m.bias, 0)
    
    def update_target_net(self):
        self.target_net.load_state_dict(self.eval_net.state_dict())

获取状态

在本节中，我们通过定义get_state方法将游戏信息抽象成3个矩阵并堆叠起来。首先，需要对游戏是否结束进行判断，这是因为当蛇头因撞到边界而结束，会导致数组越界而产生程序错误。考虑到最后一步的 并不参与参数更新，我们可以直接返回一个全0矩阵作为占位符。

def get_state(self, snake, food, done=False):
    """
    构造 3x12x12 的输入张量：
    - 通道 1：蛇头位置
    - 通道 2：蛇身（不包括蛇头）
    - 通道 3：食物位置
    """
    # 如果游戏结束，则返回一个全0的输入张量
    if done:
        return np.zeros((3, 12, 12), dtype=np.float32)

在确保存在$s^\prime$后，我们正常进行状态建模，代码如下所示：

snake_head = snake.body[0]
snake_body = snake.body[1:]
# 初始化 12x12x4 的输入张量
snake_head_matrix = np.zeros((12, 12), dtype=np.float32) # 蛇头矩阵
snake_body_matrix = np.zeros((12, 12), dtype=np.float32) # 蛇身矩阵
food_distance_matrix = np.zeros((12, 12), dtype=np.float32) # 食物距离矩阵
# 将蛇头和蛇身的位置映射到 12x12 的矩阵中
snake_head_matrix[snake_head.top // UNIT, snake_head.left // UNIT] = 1
for body in snake_body:
    snake_body_matrix[body.top // UNIT, body.left // UNIT] = 1
# 将食物位置映射到 12x12 的矩阵中
food_distance_matrix[food.rect.top // UNIT, food.rect.left // UNIT] = 1 
# 将矩阵转换为 3x12x12 的输入张量
input_tensor = np.stack([snake_head_matrix, snake_body_matrix, food_distance_matrix], axis=0)
return input_tensor

动作选择

在动作选择过程中，基本原理与Q-learning几乎一致。唯一的区别是我们将此处使用Q-table的估计更换为使用评估网络的输出。

def choose_action(self, state):
    if np.random.uniform() < self.epsilon:
        action = np.random.choice(4)
    else:
        state = torch.tensor(state, dtype=torch.float32)
        state = state.unsqueeze(0)
        action = np.argmax(self.forward(state).detach().numpy())
    return action

网络训练

网络训练的核心是通过不断地从经验回放池中采样游戏状态、动作、奖励以及下一个状态，优化评估网络的$Q$值预测，从而让智能体逐步学习到最优策略。训练过程分为三个关键步骤：存储经验、从经验中采样进行训练，以及更新目标网络的参数。
首先，通过store_transition方法，我们将智能体每一步的交互数据存储到经验回放池中。当池子中的数据量超过设定的容量上限时，最早的数据会被移除，以确保存储的经验始终是最新的。当经验回放池中存储的数据量达到批量大小时，智能体开始从中随机采样用于训练。采样到的一批数据会被拆分为状态、动作、奖励、下一状态和终止标志，并通过张量表示形式输入到网络中。在learn方法中，通过评估网络预测当前状态下智能体实际选择动作的$Q$值。智能体会通过均方误差损失函数计算评估网络的$Q$值预测与目标$Q$值之间的误差，即：

优化器根据误差对网络参数进行更新。同时，探索率会随着时间逐步衰减，从而在训练初期更多地探索新策略，而训练后期则更加依赖当前学到的策略。

此外，为了提高训练的稳定性，目标网络的参数不会频繁更新，而是通过update_target_net方法定期从评估网络复制。

def store_transition(self, s, a, r, s_, done):
    # 存储交互数据到经验回放池中。如果池子容量超过上限，则移除最早的数据。
    if len(self.replay_memory) >= DQN.MEMORY_SIZE:
        self.replay_memory.pop(0)
    self.replay_memory.append((s, a, r, s_, done))

def learn(self, s, a, r, s_, done):
    # 存储当前步的交互数据
    self.store_transition(s, a, r, s_, done)

    # 如果经验回放池中的数据不足一个批量，则不进行训练
    if len(self.replay_memory) < self.batch_size:
        return

    # 从经验回放池中随机采样一个批量的数据
    batch = random.sample(self.replay_memory, self.batch_size)
    s, a, r, s_, done = zip(*batch)
    s, a, s_, r, done = np.array(s), np.array(a), np.array(s_), np.array(r), np.array(done)

    # 转换为 PyTorch 张量
    s = torch.tensor(s, dtype=torch.float32)                # 当前状态
    a = torch.tensor(a, dtype=torch.int64)                  # 动作
    s_ = torch.tensor(s_, dtype=torch.float32)              # 下一状态
    r = torch.tensor(r, dtype=torch.float32).unsqueeze(1)   # 奖励
    done = torch.tensor(done, dtype=torch.float32)          # 是否结束

    # 使用评估网络预测 Q 值，并提取实际选择动作的 Q 值
    q_predict = self.eval_net(s).gather(1, a.unsqueeze(1))

    # 计算目标 Q 值：r + γ * max(Q(s', a'))，若终止状态则目标值为 r
    q_target = r + self.gamma * self.target_net(s_).max(1)[0].view(self.batch_size, 1) * (1 - done.unsqueeze(1))

    # 计算损失并优化评估网络
    loss = self.loss_func(q_predict, q_target)
    self.optimizer.zero_grad()
    loss.backward()
    self.optimizer.step()

    # 动态调整探索率，确保 epsilon 至少为 0.01
    self.epsilon = max(self.epsilon * self.epsilon_decay, 0.01)
    self.time_step += 1
    if self.time_step % 100 == 0: # 每100步更新一次目标网络
        self.update_target_net()

主程序修改

在基于Q-learning的主程序中，我们只需将模型修改为DQN即可。

MODEL = 'DQN'

在1500轮训练后，我们用折线图可视化其分数随轮数变化的曲线，如图3所示。相比与Q-learning算法，DQN由于其通过网络求取近似解的特性，性能提升速度明显更慢。但其具备的估计复杂状态下动作价值的能力依然使其具有非常高的研究和应用价值。

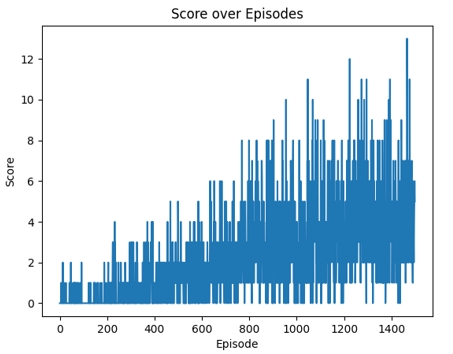
图3 DQN算法得分随轮次变化折线图

项目总结

本系列以贪吃蛇游戏为例，系统地展示了强化学习在自主游戏开发中的应用过程。从需求分析到项目设计，我们明确了游戏规则与环境搭建的基本逻辑；从Q-learning到DQN算法的逐步实现，我们详细阐述了强化学习智能体的核心原理与实现方法。通过状态建模与策略优化，智能体逐渐学会在复杂的游戏环境中做出合理的决策，展现了强化学习在高维动态环境中的强大学习能力。
在Q-learning算法部分，我们通过表格形式存储$Q$值，完成了基于离散状态和动作的策略优化。尽管Q-learning算法在小规模状态空间中表现出色，但其因状态空间扩展而导致的存储和计算限制也十分明显。为此，DQN算法通过神经网络对$Q$值进行函数近似，成功突破了Q-learning的局限性，使智能体能够应对更复杂的状态空间。我们通过经验回放和目标网络的引入，进一步提升了DQN的训练稳定性与效率，展现了深度强化学习处理连续状态问题的优势。